DFS Program in C Explained

Depth First Search (DFS) is a traversal technique used to explore all nodes or vertices in non-linear data structures like graphs and trees. In a graph, DFS explores one path as deeply as possible before backtracking, ensuring all vertices connected to the starting node are visited. In contrast, DFS for a tree follows a similar approach but assumes no cycles and a hierarchical structure, making it simpler than graph traversal. This method is widely used for tasks like pathfinding, graph traversal, and solving connectivity problems.

The depth first search C program classifies each vertex in a graph into two categories:

1. Visited: Nodes that have already been explored.
2. Not Visited: Nodes yet to be explored.

The goal of DFS is to visit every vertex in the graph while ensuring no vertex is visited more than once. So, it effectively avoids cycles.

Steps of the DFS Algorithm:

1. Start with a vertex: Choose any vertex in the graph to begin the traversal and place it on a stack.
2. Mark as visited: Pop the top vertex from the stack, mark it as visited, and record it in the visited list.
3. Explore adjacent nodes: Identify all adjacent nodes of the current vertex. Push any unvisited adjacent nodes onto the stack.
4. Repeat until the stack is empty: Continue popping vertices from the stack, marking them as visited, and adding their unvisited neighbours until the stack is completely empty.

Now let’s take a look at an example of how DFS algorithm in C works: 

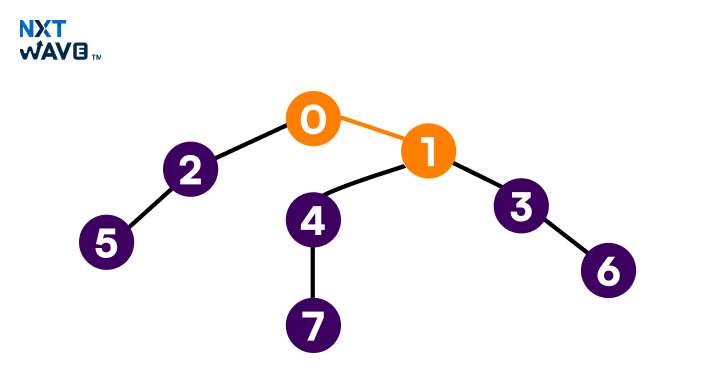
Consider this undirected graph with 8 vertices.

In this state, we have visited zero and marked it green. Node zero has two non-visited neighbours 1,2. We’ll move to node 1.

Visited [0] Stack[0], move to vertex 1

In this step, we’ll mark 1 as visited. But node 1 has two unvisited vertices: 3 and 4. We’ll move to 3.

Visited [0,1] Stack [0,10]

Move to vertex 3

In this step, we’ve moved to 3 and marked it.

Visited [0,1,3] Stack [0,1,3]

Move to vertex 6

In this step, we’ve moved to vertex 6 and marked it. Now we’ll have to move back.

Visited [0,1,3,6] Stack [0,1,3,6]

Backtrack to vertex 3, then to vertex 1, then to vertex 4.

Now we move to the vertex 4 branch and continue down.

Visited [0,1,3,6,4] Stack [0,1,4]

Move to vertex 7

Now we move to the last node on the branch which is 7.

Visited [ 0,1,3,6,4,7] Stack [0,1,4,7]

backtrack to vertex 4, then to vertex 1, then to vertex 0, then move to vertex 2

From here we mark 2 and continue on the branch.

Visited [0,1,3,6,4,7,2] Stack [0,2]

Move to vertex 5

Now we move to the last node 5.

Visited [0,1,3,6,4,7,2,5] Stack [0,2,5]

Final state

Let’s take a look at the pseudocode DFS program in C:

DFS(G, u):  
    u.visited = true  
    for each v ∈ G.Adj[u]:  
        if v.visited == false:  
            DFS(G, v)  

init():  
    for each u ∈ G:  
        u.visited = false  
    for each u ∈ G:  
        DFS(G, u)  

The pseudocode for DFS is shown below. In the init() function, the DFS function is executed for every node in the graph. This is particularly important because graphs may contain disconnected components, which means some vertices might not be reachable from others. By running the DFS algorithm on each node, it makes sure that every vertex in the graph is visited. This is regardless of whether the graph is connected or has isolated parts. It guarantees complete traversal of the graph

The example of a DFS program in C with output is as follows:

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>  // Added this line for malloc
// Graph DFS Implementation
#define MAX_VERTICES 8
// Adjacency Matrix Representation
int graph[MAX_VERTICES][MAX_VERTICES] = {
    {0, 1, 1, 0, 0, 0, 0, 0},
    {1, 0, 0, 1, 1, 0, 0, 0},
    {1, 0, 0, 0, 0, 1, 0, 0},
    {0, 1, 0, 0, 0, 0, 1, 0},
    {0, 1, 0, 0, 0, 0, 1, 0},
    {0, 0, 1, 0, 0, 0, 0, 0},
    {0, 0, 0, 1, 1, 0, 0, 1},
    {0, 0, 0, 0, 0, 0, 1, 0}
};
bool visited[MAX_VERTICES] = {false};
// Graph DFS Function
void graphDFS(int vertex) {
    // Mark current vertex as visited
    visited[vertex] = true;
    printf("%d ", vertex);

    // Explore all adjacent vertices
    for (int i = 0; i < MAX_VERTICES; i++) {
        if (graph[vertex][i] == 1 && !visited[i]) {
            graphDFS(i);
        }
    }
}

// Tree DFS Implementation
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// Create a new tree node
struct TreeNode* createNode(int data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// Tree DFS (Pre-order Traversal)
void treeDFS(struct TreeNode* root) {
    if (root == NULL) return;

    // Visit root
    printf("%d ", root->data);

    // Traverse left subtree
    treeDFS(root->left);

    // Traverse right subtree
    treeDFS(root->right);
}

int main() {
    // Graph DFS Demonstration
    printf("Graph DFS Traversal: ");
    graphDFS(0);  // Start DFS from vertex 0
    printf("\n");

    // Reset visited array for multiple traversals
    for (int i = 0; i < MAX_VERTICES; i++) {
        visited[i] = false;
    }

    // Tree DFS Demonstration
    // Create a sample tree
    struct TreeNode* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);
    root->right->left = createNode(6);
    root->right->right = createNode(7);

    printf("Tree DFS (Pre-order) Traversal: ");
    treeDFS(root);
    printf("\n");

    return 0;
}

Output:

Graph DFS Traversal: 0 1 3 6 4 7 2 5 
Tree DFS (Pre-order) Traversal: 1 2 3 4 5 6 7 

The DFS algorithm has diverse applications in graphing and beyond:

• Pathfinding: DFS can determine whether a path exists between two nodes. It explores all possible routes in weighted or unweighted graphs.
• Checking Bipartite Graphs: It helps verify if a graph can be divided into two sets such that no vertices within the same set are adjacent.
• Finding Strongly Connected Components: DFS is integral to algorithms like Kosaraju’s and Tarjan’s for identifying strongly connected components in directed graphs.
• Cycle Detection: By tracking visited nodes and recursion stacks, DFS can detect cycles in both directed and undirected graphs.
• Topological Sorting: In directed acyclic graphs (DAGs), DFS enables topological sorting, which is essential for scheduling and dependency management.
• Solving Puzzles: The DFS algorithm in C is used to explore solutions in problems like mazes, Sudoku, and other puzzles.

Depth First Search (DFS) is a foundational concept with applications in multiple domains like networking, AI, and problem-solving in software systems. For budding software engineers, mastering DFS is essential because it builds critical thinking and problem-solving skills required to tackle complex, real-world scenarios. Writing a DFS program in C goes beyond coding and goes into understanding data structures like graphs and trees, which are at the core of modern computing. This hands-on experience strengthens your ability to approach challenges logically and optimize solutions. Both of these skills are critical as you step into a professional software development career. To build a solid foundation, join the CCBP 4.0 Academy program and become job-ready!

1. What is the main use of the DFS algorithm in graphs?

DFS explores all vertices of a graph by traversing as deeply as possible along each branch before backtracking.

2. How is DFS different from BFS in graph traversal?

DFS focuses on depth-first exploration. BFS (Breadth First Search) explores all neighbours at the current depth before moving deeper.

3. Why is recursion commonly used in implementing DFS?

Recursion naturally mirrors the backtracking process of DFS. Therefore, it makes the implementation simpler and more intuitive for traversing graph paths.

4. Can DFS detect cycles in a graph?

Yes, DFS can identify cycles by checking for back edges in directed graphs or revisiting nodes in undirected graphs.

5. What are the common applications of DFS?

DFS is used for pathfinding, cycle detection, finding connected components, solving puzzles, and performing topological sorting in tasks like dependency resolution.